
문제 상황
Given a sorted integer array nums and an integer n, add/patch elements to the array such that any number in the range [1, n] inclusive can be formed by the sum of some elements in the array.
Return the minimum number of patches required.
nums의 정렬 배열이 있고 n이라는 정수를 추가할 거임, 요소를 add/patch 한다, 1부터 n까지의 모든 수를 배열안의 수로 제작할 수 있게 되는 최소의 변형 수를 구하는 문제
입력
1 <= nums.length <= 10001 <= nums[i] <= 104numsis sorted in ascending order.1 <= n <= 2^31 - 1
출력
배열의 조합으로 [1 … n]까지의 정수를 만들 수 있는 최소의 개수
과정
무조건 최소의 수는 2진법 자리수다
하지만 문제는 이미 존재하는 배열에 추가하는 것이기 때문에 정확히 그 31개의 2의 배수들이 있는것과 동일한건지는 알 수 없었다.문제의 답이 31이하라는건 분명한사실이지만 2진수 덧셈을 맞추는 방식으로 문제를 해결하려면
2진수가 아닌 수와 2진수의 여분들의 조합이 해당 부족한 2진수를 만들 수 있는건지를 확인해야한다. 그런데 이 상황은 경우에 따라서 다르기 때문에 어떻게 풀어야할지가 난감했다.
그리디로 문제 해결

점화식으로 접근을 했을 때 이런 결과다. n - 1 번째의 요소까지들이 g(x)를 만족한다고 했다면 n번째 인덱스 x에 대해서도 g(S(x)) 이 성립한다고 말할 수 있을 경우를 찾으면 된다.

가정한대로 S(Xn -1)은 1부터 S(Xn - 1) 까지 모든 수를 구현 가능하다.
그러면 S(Xn - 1) + 1 부터 S(Xn - 1) + Xn 까지의 모든 수들은
S(Xn - 1)에서 적절한 수 k를 조합해서 만들어서 빼고 거기에 Xn을 더한다는 방식으로 구현하는게 가능하다. 식으로 따지면 위의 식이다.
그럼 이제 점화식을 불가능하게할 조건은 Xn 이 S(Xn - 1)보다 클 때 밖에 없다는걸 알 수 있다. 그때가 바로 요소를 추가해야할 때이다. 그럼 이제 어떤 요소를 추가해야하는가? 가 또다른 중요한 점이었다.

여기서 이제 add/patch를 한다. 그런데 이제 어떤 값을 해야할까? 여기서 그리디 개념이 들어간다 S(x n - 1) 보다 1 큰 수를 저장하기만 된다.
이제 맨처음 착각했던 비트마스킹을 생각해보면 정확히 이 논리로 진행된다는 것을 알 수 있다.

S(x2)까지의 값은 7이다 그리고 x3의 값이 8이어도 g(15)를 만족한다는 것을 알 수 있다.
알고리즘 개요도
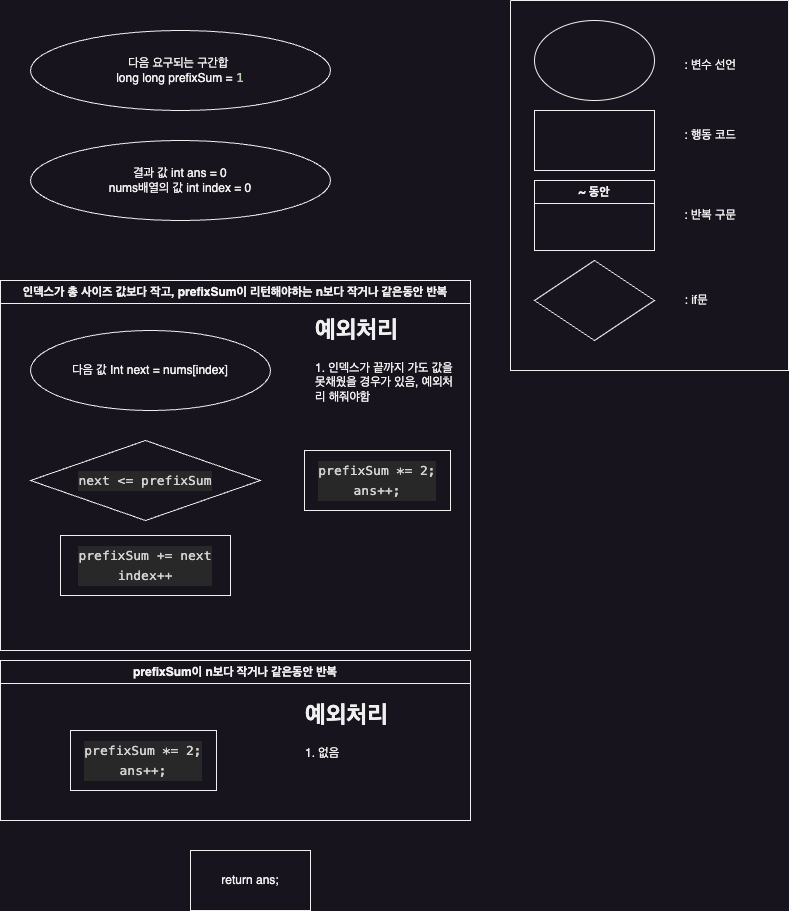
알고리즘
class Solution {
typedef long long ll;
public:
int minPatches(vector<int>& nums, int n) {
ll prefixSum = 1;
int ans = 0;
int index = 0;
while (index < nums.size() && prefixSum <= n)
{
int next = nums[index];
if (next <= prefixSum)
{
prefixSum += next;
index++;
} else {
prefixSum *= 2;
ans++;
}
}
while (prefixSum <= n)
{
ans++;
prefixSum *= 2;
}
return ans;
}
};'알고리즘연구소👨💻 > 리트코드' 카테고리의 다른 글
| [Leetcode 1052번 문제] 1052. Grumpy Bookstore Owner (0) | 2024.06.21 |
|---|---|
| [Leetcode 826번 문제] 826. Most Profit Assigning Work (0) | 2024.06.18 |
| [Leetcode 633번 문제] 633. Sum of Square Numbers (0) | 2024.06.17 |
| [Leetcode 648번 문제] 648. Replace Words (0) | 2024.06.07 |
| [Leetcode 2370번 문제] 2370. Longest Ideal Subsequence (0) | 2024.05.05 |



